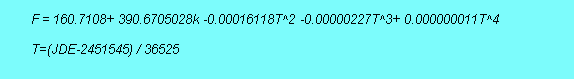|
 |
|||||||||
|
||||||||||
Lunar eclipses occur when Earth’s shadow falls on the Moon. There are about 150 lunar eclipses per century. Lunar eclipses can occur only at full moon, and can be either total or partial. Further they can be umbral and or penumbral. Total lunar eclipses can last up to 2 hours, while partial lunar eclipses can last up to 4 hours. Any observer on dark face of earth can see when lunar eclipse when it occurs, but solar eclipses are not so. During period 3500BC to 700 BC, nearly 4350 lunar eclipses have probably occurred. A good fraction of these would have been visible in Kuruxethra. Lunar eclipse can be roughly predicted by, [Ref-6]. Julian day of Lunar eclipse=2449128.59+29.53058867n +/-0.25 Where n is a half-integer. Lunar Eclipses occur when n (mod 223) is one of 0.5, 6.5, 12.5, 23.5, 35.5, 41.5, 47.5, 53.5, 76.5, 82.5, 88.5, 94.5, 100.5, 123.5, 129.5, 135.5, 141.5, 158.5, 164.5, 170.5, 176.5, 182.5, 188.5, 205.5, 211.5, or 217.5. The sequence of eclipses repeats with a period of 223 months Saros Cycle. Solar Eclipse occurs when Moon’s shadow falls on earth observer. About 240 solar eclipses occur every century. During period 3500BC to 700 BC, nearly 6960 Solar Eclipses have occurred. Solar eclipses take place during daylight hours and can occur only at new moon. Solar eclipses may be total or annular. Total solar eclipses can last up to about 8 minutes, and partial solar eclipses can last up to 115minutes. The shadow of moon has a limited size of one to two thousand miles falling on nearly 8000-mile diameter earth. Hence, solar eclipses can be seen in a limited range of longitude-latitude where the shadow falls. Julian Day of Solar eclipse= 2449128.59+29.53058867n +/-0.25 During the period of our interest of 3500BC to 700 BC, nearly 4350 Lunar Eclipses and 6960 solar eclipses have occurred. We need to search amongst these for eclipse pairs visible in Kuruxethra, which occurred in 13 days. Though solar eclipses are more in number, from a given location like Kuruxethra, they are relatively fewer solar eclipses seen because of limited moon shadow size, while all the lunar eclipses are visible. Hence for an observer at a given location, lunar eclipses appear to be more. We are more interested in eclipse pairs, occurring during consecutive new moon/ full moon period that could be seen at Kuruxethra. While the Saros cycle concept gives us a gross feeling for number of eclipses that may have occurred, we need more precise computation for determining Mahabharata eclipses. Jean Meeus [Ref-7] provides numerical algorithms, which take in to account many periodic terms in Moon’s longitude, latitude, and distance from earth. His algorithms calculate light traverse time, Moon’s argument latitude, sun’s mean anomaly, Moon’s mean anomaly and mean distance of moon from its ascending node. He also corrects for eccentricity of earth’s orbit around Sun, which is decreasing with time. His algorithms have many parameters and dimensions, but one simple identity that can be used for estimating possibility of an eclipse is given below. [Ref-4]
k is an integer, 1 for New Moon & 0.5 for Full Moon JDE corresponds to Julian Ephemeris Day. If F is near zero or 360 (or multiples) then an eclipse will occur near Moon’s ascending node. If F is near 180, then the eclipse takes place near descending node of Moon. This class of computation can assist in determining a lunar/solar eclipse somewhere on earth. Subsequently the earth’s observer location has to be considered based on precise Time of Julian day. This class of calculations are embedded in many software code currently available on market. Considerable validation is required Eclipse evaluating computational software and its validation in present context Astronomical calculations have been greatly improved since past 30 years, particularly with considerable amount of trajectory work conducted in Moon and other scientific projects. High accuracy computer models and software have been developed. These are validated against databases from US Naval Observatory’s Interactive computer Ephemeris, and Jet Propulsion Laboratory in California. One such code is LodeStar Pro copy righted by Wayne C Annala in 1994. [Ref- 8] Its accuracy has been stated as about 0.9 deg in moon position between 2000BC and 4000 BC. This would correspond to about 3-4 minutes time error in eclipse time uniformly if it is along the ecliptic. If the error is orthogonal to ecliptic, eclipse will not occur. Effort has been made to validate and develop confidence in the LodeStar Pro by checking for historical eclipses of 1000-2500 BC from clay tablet records from Mesopotamia area. A large number of clay tablets with eclipse data has been available and has been a subject of analyses and study. These not only detail eclipses but also provide concurrent planetary position data.
|
||||||||||||